😎

알고리즘 문제 풀이 팁

그리디 알고리즘

구현

Upper bound / Lower bound

아래 강의 수강 후 정리한 내용이 다수 존재합니다.

이것이 취업을 위한 코딩 테스트다 with 파이썬

취업과 이직을 결정하는 알고리즘 인터뷰 완벽 가이드, C/C++, 자바 코드 제공 - https://www.hanbit.co.kr/store/books/look.php?p_code=B8945183661

https://www.youtube.com/playlist?list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81

그리디 알고리즘

기본적인 의미는 탐욕(그리디) 알고리즘이다.

즉 현재 상황을 기준으로, 가장 좋은 방법을 선택하는 것이다.

내가 생각한 그 좋은 방법이 매번 반복적으로 선택할 때 최적의 해를 구할 수 있는 방법인지 확인해야한다.

몇 문제를 풀어보니, 나열된 값의 정렬이 매우 중요하다.

즉, 경우의 수(주어질 지, 내가 만들어야될지는 모르겠지만)를 잘 정렬하여 현재 상황이 원하는 순서대로 나타날 수 있도록 해야한다.

예시를 들어보자.

보통 드라이버 세트를 사면 옆 사진처럼 사용할 수 있는 나사의 크기별로 드라이버가 순서대로 들어있다.

어떤 드라이버는 안경용으로 사용되는 매우 작은 나사를 조절할 때 사용할 수 도 있다.

또 어떤 드라이버는 가구 등을 조립할 때 사용하는 큰 나사를 조절할 때 사용하는 드라이버가 있을 수 있다.

근데 우리가 눈으로 나사를 보면 바로 어떤 드라이버가 맞는지 알기 어려울거다.

그래서 우리는 나사와 맞는 모양을 찾고, 크기순으로 하나씩 끼워보며 확인한다.

만약 드라이버가 크기별로 정리되어 있지 않는다면, 적합한 드라이버를 빠른시간에 찾기 어려울 것이다.

만약 잘 정돈되어 있다면, 우리가 원하는 현재 상황은 아래와 같을 것이다.

•

작은 드라이버 → 큰 드라이버

•

큰 드라이버 → 작은 드라이버

그리디 알고리즘도 마찬가지다.

경우의 수가 마구 섞여 있다면, 매 순서대로 최적의 방법을 찾는 그리디 알고리즘을 제대로 동작할 수 없다.

구현

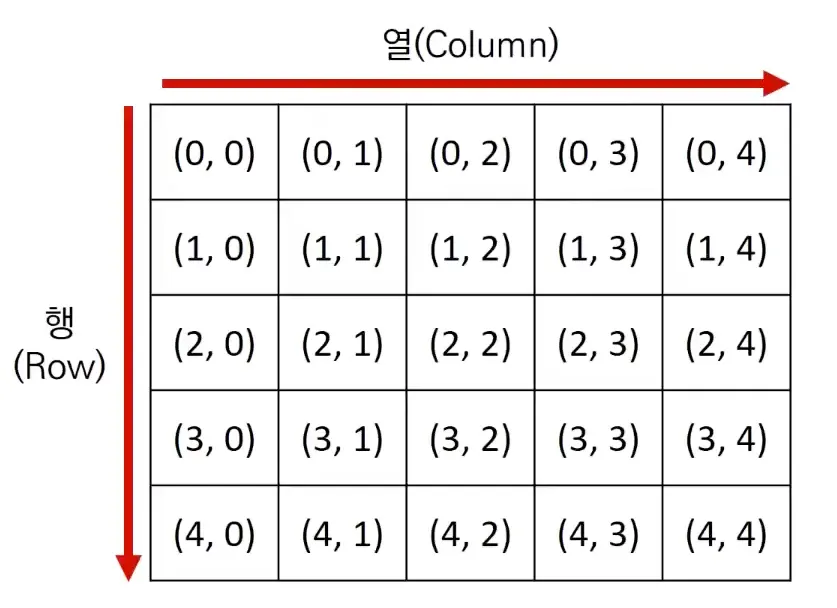
시뮬레이션이나 탐색 문제는 2차원 공간에서 방향 벡터를 자주 사용한다.

일반적으로 알고리즘의 2차원 공간은 행렬(Matrix)의 의미를 가지고 사용된다.

이 행렬은 (0, 0) 부터 시작된다.

출처 : 유튜브 “[이것이 코딩 테스트다 with Python] 14강 구현 유형 개요” 강의 중

정사각형 형태의 행렬 회전

N \times N

형태의 행렬을 시계방향/반시계방향으로 회전하는 함수이다.

개인적으로 함수를 사용한 코드는 원리를 이해할 때만 확인하고, python에서는 slice와 zip을 이용한 함수를 쓰는데 더 좋다.

왜냐하면

N \times N

형태 뿐 아니라,

M \times N

형태와 같이 행과 열의 길이가 달라도 사용이 가능하기 때문이다.

함수를 사용한 예시 코드 (개념만)

리스트 slice와 zip을 이용한 예시 코드 (추천)

DFS (깊이 우선 탐색)

설계

주로 재귀함수 방식과 스택을 자주 사용한다.

하나의 기준에서 조건에 맞는 노드를 계속 연결하여 찾기 때문이다.

따라서 재귀로 DFS를 구현할 때, 함수 시작 부분에 중단 조건을 반드시 설정해줘야 한다.

크게 아래와 같은 느낌으로 설계하면 편하다.

def dfs(...):

	# 탐색 종료 조건
	if 탐색 종료 조건:
        return False
    
  if 추가 탐색 가능 조건:

      # 해당 위치(노드)에 방문했음을 기록하는 코드(문제에 따라 선택)
      ...

      # 탐색할 범위의 재귀함수 동작
      dfs(...)
      dfs(...)
      dfs(...)

      # 이 부분까지 왔다면, 중간에 멈추지 않고 끝까지 탐색을 마친 경우이다.
      return True
  
  # 추가 탐색 가능 조건에 맞지 않을 때:
  return False
Python
복사

위 dfs(...) 함수를 아래처럼 사용할 수 있다.

dfs(...) 사용 시 인자는 다를 수 있다.

...

for i in range(N):
	for j in range(M):
		if dfs(i, j) == True: 
			탐색 완료 시 동작 코드
Python
복사

함수 호출 횟수 조정

DFS에서 재귀함수를 사용할 때, 예시에 따라 기본적으로 한정한 재귀 깊이를 넘어서도록 재귀 함수를 호출할 때가 있다. 이때는 RecursionError 를 발생시킬 수 있다.

백준에서 작성한 에러 관련 내용을 살펴보면 백준의 채점 서버에서 정한 기본적인 재귀 깊이는 1000이기 때문에, 그 이상 재귀를 사용하게 되는 예시는 에러를 뱉는다고 한다.

현재 사용하는 IDE에서도 아래처럼 확인이 가능한데, 본인도 1000이 나왔다.

import sys

# 1000
print(sys.getrecursionlimit())
Python
복사

아래와 같이 sys모듈의 setrecursionlimit() 메서드를 사용하여 수치 조정이 가능하다.

보통은

10^{6}

이나

10^{9}

값으로 설정한다고 하는데, 아무리 크게 잡아도 채점 서버가 감당할 수 없어질 정도로 깊어지면 Segmentation fault 가 발생해 런타임 에러 이유로 SegFault를 받게된다고 한다.

import sys
sys.setrecursionlimit(10**6)

...
Python
복사

아무튼 위와 같이 수정하면 아래 이미지처럼 정상적으로 채점이 진행된다.

•

RecursionError 관련 내용

런타임 에러 (RecursionError)

RecursionError는 재귀와 관련된 에러입니다. 가장 많이 발생하는 이유는 Python이 정한 최대 재귀 깊이보다 재귀의 깊이가 더 깊어질 때입니다. Python이 정한 최대 재귀 깊이는 sys.getrecursionlimit() 을 이용해 확인할 수 있습니다. BOJ의 채점 서버에서 이 값은 1,000으로 되어 있습니다. 소스 1. n을 입력받고, 1부터 n까지 합을 재귀 함수로 구하는 소스 calc(n)을 호출하면 총 n+1번의 재귀 호출이 발생합니다.

https://help.acmicpc.net/judge/rte/RecursionError

BFS (넓이 우선 탐색)

주로 큐와 while 함수를 자주 사용한다.

DFS가 하나의 위치에서 조건에 맞는 위치(노드)를 끝까지 탐색했다면, BFS는 하나의 위치에서 인접한 여러 위치(노드)들이 조건에 맞는지를 우선 확인한다.

간단히 말하면 긴 밧줄과 그물과 같은 차이라고 보면 된다.

마찬가지로 함수 초반에 탐색을 중단하는 코드가 반드시 있어야 된다.

from collections import deque

# 예시로 x,y 인자를 넣어준 것
def bfs(x, y):
    
    # 처음 노드를 초기값으로 넣어준다.
    queue = deque([(x,y)])

    # 큐에 값이 들어있다면 계속 반복
    while queue:
        
        # 큐에서 값 먼저 꺼내기
        K = queue.popleft()

        # 꺼낸 값이 탐색을 진행할 수 없는 조건인지
        if 탐색 불가능 조건:
            break
        
        # 주변의 위치(노드)들이 탐색할 조건에 맞는지
        # 현재 위치(노드)에서 값을 조정하여 주변의 위치(노드)의 값을 확인한다.
        if 주변 노드 값 비교 조건:
            queue.append(주변 노드 값)
            주변 노드의 값을 변경하여, 방문했는지 여부를 설정하거나 몇 번 이 노드를 조회했는지 값을 설정할 수 있다.

        ...더 많은 주변 노드 탐색 조건 추가
Python
복사

위 bfs(...) 함수를 아래처럼 사용할 수 있다.

함수안에서 while로 동작하는 경우 밖에서는 한번만 동작시키면 된다.

Python
복사

•

만약 특정 2차원 공간에서 최단거리를 구하는 문제일경우, 각 노드에 방문할때마다 노드의 방문 횟수를 기록하면 편하게 최단거리를 구할 수 있다.

확률과 통계에서 배우는 최단거리를 검색하면 더 이해가 빠르게 가능하다.

•

특정 조건들의 상태에 따라, 별도로 벡터의 상태를 기록해야될 때는 배열을 한차원 더 만들어주면 된다.

상태 값에 따라 함수의 진행이 달라지며, 각 좌표에 반영되는 시점도 다르기 때문이다.

예시로 백준에는 벽 부수기 라는 문제가 있는데, 이 문제에서는 벽 부수기를 사용했는지 여부에 따라 각 좌표의 값이 다르다.

DFS / BFS 공통

각 노드의 연결 정보 정리

문제에서 각 노드의 연결정보를 [ A, B ] 형태의 원소 값이 모인 리스트로 제시해주는 경우가 있다.

이때는 각 노드가 어떤 노드와 연결되었는지 한눈에 확인하기가 불편하다. 아래와 같이 가공하여 문제를 풀면 편하다.

sort()로 정렬을 해준 이유는 더 빠른 탐색을 위해서이다.

# 첫 줄은 각각 정점의 개수와 간선의 개수를 나타낸다. (정점 개수 -> 6 / 간선 개수 -> 5)
6 5
1 2
2 3
4 5
6 3
5 3
Plain Text
복사

# 기존 방법
graph = [list(map(int, input().split())) for _ in range(M)]

# [
# 	[1, 2],
# 	[2, 3],
# 	[4, 5],
#   [6, 3],
#   [5, 3]
# ]
print(graph)

# 각 노드별로 연결 노드 저장
graph = [[] for _ in range(N+1)]

for _ in range(M):
    a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)
    graph[a].sort()
    graph[b].sort()

# [[],[2],[1, 3],[2, 5, 6],[5],[3, 4],[3]]
print(graph)
Python
복사

Upper bound / Lower bound

오름차순으로 정렬된 숫자들로 이루어진 배열에서, 특정 값(target)보다 큰 / 크거나 같은 값이 존재하는 첫 위치를 찾을 때 사용한다.

•

Upper bound : 배열에서 특정 값(target)보다 큰 값이 존재하는 첫 위치를 찾는다.

예시

•

Lower bound : 배열에서 특정 값(target)보다 크거나 같은 값(이상)이 존재하는 첫 위치를 찾는다.

예시

이분탐색

이분탐색 문제를 결정 문제로 변경해야하는 경우가 있다. 특정 조건을 만족하는 최소 시간의

t

값을 찾는 경우이다.

이는 단순히 시간이 아닌 다른 값일 수 있다. 예시를 위해 시간으로 예시를 들었다.

시간 T<tT < tT<t 일 때는 TTT 가 모두 조건에 만족하지 않는다.

시간 T≥tT \ge tT≥t 일 때는 TTT 가 모두 조건에 만족한다.

•

“조건 AAA 를 만족하는 최소 시간 ttt 를 찾아라” 조건의 문제일 경우 

최소 시간 TminT_{min}Tmin​ 과 TmaxT_{max}Tmax​ 를 구한다. 보통 최소 시간은 0으로 잡는다.

이분탐색으로 TmidT_{mid}Tmid​ 를 구하여 해당 시간 TmidT_{mid}Tmid​ 가 조건에 만족하는지 확인한다.

TmidT_{mid}Tmid​ 시간이 조건에 만족한다면 더 작은 TmidT_{mid}Tmid​ 를, 만족하지 않는다면 더 큰 TmidT_{mid}Tmid​ 를 구한다.

물론 거꾸로 “조건

A

를 만족하는 최대 시간

t

를 찾아라” 조건의 문제도 동일하게 풀면된다.

DP(다이나믹 프로그래밍)

기본적인 방법으로 하나의 큰 문제를 여러 개의 작은 문제로 나눈다. 나눈 문제들의 결과를 저장하여, 큰 문제를 해결할 때 결과값을 사용한다.

문제를 해결할 수 있는 방법을 찾는다. → DP에서는 점화식을 잘 구하는게 필수다.

하나의 큰 문제를 1번의 해결법(점화식)이 적용되는 범위 단위로 나눈다.

2번에서 나뉜 각 문제의 결과를 구한 후, 더 큰 단위의 문제를 해결할 때 결과값을 재활용한다.

이 방법을 사용하는 이유는, 하나의 큰 문제를 일반적인 재귀로 구하면 동일한 문제의 결과를 이미 구했음에도 계속 반복해서 구하기 때문이다.

자주 사용되는 예시로 피보나치 수열을 일반적인 재귀 vs DP 방식으로 비교해보겠다.

재귀예시

DP예시

위 예시의 결과에서 DP가 재귀보다 154083.5 배 정도 빠른것을 알 수 있다.

그만큼 재귀 → DP로 해결이 가능하다면, 매우 효율적으로 같은 결과를 구할 수 있는것이다.

이러한 DP도 2가지 방법으로 나뉘는데, Top-Bottom 방식과 Bottom-Up 방식이다.

적용되는 알고리즘이 다르다. 뭐 그런건 아니고, DP를 동작하는 방식의 차이이다.

같은 DP문제라도 두 방법 중 잘고르면 난이도가 많이 달라질 수 있으니, 두 방법 모두 잘 숙지해야한다.

Top-Bottom 방식

위에서 → 아래로, 하향식이라고 생각하면 편하다. 큰 문제 해결을 위해, 작은 문제를 해결하는 방법이다.

이것은 보통 재귀를 사용하지만, DP기 때문에 이전 계산 결과를 별도로 저장하는것이 일반적인 재귀와의 차이점이다.

예시로 이전의 피보나치 수열을 Top-Bottom 방식으로 만들어보자.

Top-Bottom 방식은 함수가 재귀로 돌아가기 때문에, 함수안에 결과를 저장할 공간을 선언하기 어렵다.

처음에 fibonacci_top_down(n)으로 시작한다.

fibonacci_top_down(n) 호출 시, fibonacci_top_down(n)에서 fibonacci_top_down(n-1), fibonacci_top_down(n-2) 이 호출된다.

이런 방식으로 가장 큰 단위의 fibonacci_top_down(n) 에서 점점 작은 단위인 문제들로 해결하는 방식이다.

N = 35
dp = [0] * (N+1)
dp[1] = 1

def fibonacci_top_down(n):

    if dp[n] == 0 and n > 1:
        # 재귀
        dp[n] = fibonacci_top_down(n - 1) + fibonacci_top_down(n - 2)

    return dp[n]
Python
복사

Bottom-Top 방식

아래에서 → 위로, 상향식이라고 생각하면 편하다. 가장 작은 문제들부터 답을 먼저 구해버리고, 가장 마지막에 큰 단위의 문제를 해결한다.

그럼 Top-Bottom 방식과 차이가 없는거 아냐? 라고 생각하겠지만, 조금 다르다.

Top-Bottom 방식은 Top → Bottom 방향으로 재귀가 진행되며, 재귀가 진행되지 않는 구간까지 도달한 후 return되며 → Top으로 올라오는 방식이다.

반면 Bottom-Top은 그냥 무조건 가장 작은 문제에서 시작을 해버린다. 즉, 재귀로 탐색하는 과정이 없다.

마찬가지로 피보나치 수열을 Bottom-Top 방식으로 만들어보자.

우선 설명대로 재귀로 동작하지 않는다. 그리고 점화식(문제 해결법)이 적용되는 가장 작은 문제인 fibonacci(2)부터 → fibonacci(n) 순서로 값을 기록한다.

작은 단위의 문제가 먼저 해결되기 때문에, 점점 커진 단위의 문제들은 이전의 작은 단위의 문제 결과를 사용하기만 하면된다.

def fibonacci_bottom_top(n):
    
    # 재귀로 동작하지 않기 때문에, 내부에 결과 저장 공간을 선언해도 된다.
    dp = [0] * (n + 1)
    
    # fibonacci(1) = 1
    dp[1] = 1
    
    # 이미 값이 존재하는 경우
    if dp[n] > 0 and n > 1:
        return dp[n]
    else:
        # 2 ~ n 순서로 값을 구한다.
        # 2가 점화식이 적용되는 최소 값이기 때문에, 가장 작은 단위의 문제인 fibonacci(2)부터 구한다.
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] + dp[i - 2]

    return dp[n]
Python
복사

•

출처

Top-down 방식과 Bottom-up 방식

다이나믹 프로그래밍 문제를 푸는 방법으로는 크게 두 가지, Top-down 방식과 Bottom-up 방식 이 있다. 이 두 방식은 어떠한 차이점이 있는지 피보나치 숫자의 예시와 함께 알아보자. 다이나믹 프로그래밍 문제를 풀 때는 이 두 방식 중 '어느 것이 더 낫다'고 콕 집어서 말하기가 힘든 것 같다. 문제들 중에는 두 방식의 구현 난이도가 굉장히 다른 경우 가 존재하기도 한다.

https://velog.io/@chnh506/Top-down-%EB%B0%A9%EC%8B%9D%EA%B3%BC-Bottom-up-%EB%B0%A9%EC%8B%9D

알고리즘 / 풀이법 구분

•

출처

코딩테스트 팁 (python)

1. 아스키코드 변환 ord(value) # 역으로는 chr 2. 조합 from itertools import combinations from itertools import permutations list(map(''.join,combinations( arr , 1 ))) 3. 절대값 abs(value) 4. 문자열 리스트 합치기 text = ''.join(arr) 5. 최대 공약수 import math math.gcd(21, 14) #7 6. 펙토리얼 factorial import math math.factorial(5) #120 7.

https://velog.io/@tlsehguddn23/%EB%AC%B8%EC%A0%9C-%EC%A0%95%EB%A6%AC

특정 범위를 계산하는 문제

•

추석트래픽 : https://programmers.co.kr/learn/courses/30/lessons/17676

•

단속카메라 : https://programmers.co.kr/learn/courses/30/lessons/42884

위와 같이 타임라인 형식으로 나타내는 표에서 특정 범위에 속하는 조건을 주어졌을때는, 각 경우의 시작과 끝 부분을 이용한다.

예시로 A 경우와 B 경우가 겹치는 부분이 있는 경우 → A 시작 ≤ B 시작 or B끝 ≤ A 끝 / B 시작 ≤ A 시작 or A끝 ≤ B 끝 인것을 확인하면 된다.