Search
✏️

알고리즘 정리

코딩 테스트를 위한 알고리즘 & 자료구조 공부를 정리한 내용입니다. 또한, 대부분의 내용이 Python 언어로 정리되어 있습니다. 파이썬에 대한 정리를 확인하고 싶다면 아래 링크로 접속해주세요!
PYTHON 기본 문법 정리
목차

정리한 강의 소개

프로그래머스 사이트의 [ 어서와! 자료구조와 알고리즘은 처음이지? ] 강좌를 수강하고, 개인적으로 정리한 내용이 있음을 알려드립니다.
실습 예시를 풀어보며 공부가 잘되기 때문에 실습 예시를 풀며 공부를 원하시거나 더 자세한 내용을 원하시면 아래 사이트에서 직접 수강을 권장드립니다.
어서와! 자료구조와 알고리즘은 처음이지?
× 이 강의는 Python 기반으로 진행하므로 최소한 문법에는 익숙한 상태로 수강해야 합니다. 듣고는 싶은데, Python을 잘 모르나요? 이 무료 강의 부터 듣고 수강하세요. 한 단계 더 도약하고 싶은 비전공자 출신의 개발자, 또는 개발자 꿈나무 모두에게 추천하는 강의.한 손엔 파이썬, 한 손엔 자료구조와 알고리즘을 확실히 무기로 쥐세요. 어서와!
https://programmers.co.kr/learn/courses/57
두 번째로 나동빈님의 [ 이것이 취업을 위한 코딩 테스트다 with 파이썬 ] 강좌를 수강하고 정리한 내용도 포함되어 있습니다.
이것이 취업을 위한 코딩 테스트다 with 파이썬
취업과 이직을 결정하는 알고리즘 인터뷰 완벽 가이드, C/C++, 자바 코드 제공 - https://www.hanbit.co.kr/store/books/look.php?p_code=B8945183661
https://www.youtube.com/playlist?list=PLVsNizTWUw7H9_of5YCB0FmsSc-K44y81

1. 선형 배열(Linear Array)

배열(리스트) : 같은 자료형을 가진 데이터가 연속적으로 저장된 자료구조
Array는 논리적 저장 순서와 물리적 저장 순서가 일치하기 때문에, 인덱스를 사용한 직접 접근이 가능하다.
“논리적 저장 순서와 물리적 저장 순서가 일치” → 배열의 각 요소가 메모리상에서 연속적으로 저장된다는 의미

리스트 관련 메서드

메서드는 아니지만, array[index] 를 통한 접근은 (O(1)O(1)) 이다.
•
list.append(iterable) : 맨 뒤에 원소로 그대로 덧붙이기
◦
평균적으로는 (O(1)O(1))
◦
하지만 동적 배열 형태를 사용하는 Python에서는 초기에 할당된 크기에서 더 큰 메모리 공간이 필요한 경우, 더 큰 크기로 확장된다.
◦
이 경우, 기존 요소를 더 큰 공간의 메모리 공간으로 복사하는 작업이 필요하다.
◦
이 경우에는 (O(n)O(n)) 이 될 수 있다.
•
list.extend(iterable) : 맨 뒤에 원소로 추가하기
◦
추가되는 요소의 갯수가 m개일 경우, (O(m)O(m)) 이 된다.
•
list.pop() : 맨 뒤의 원소 하나를 꺼내기
◦
별도의 인덱스를 지정하지 않았다면, 가장 마지막 요소를 제거하기 때문에 (O(1)O(1))이다.
◦
하지만, 별도의 인덱스를 지정하여 pop을 했다면 pop과정 후 추가적인 shift 작업이 필요하다.
◦
이 경우, (O(n)O(n)) 이 될 수 있다.
append와 extend 메서드 차이
리스트 길이와 실행 시간이 비례하는 메서드 (O(n)O(n))
•
list.insert(index, iterable) : 특정 위치에 원소 추가
•
del(index)/ del list[index] : 특정 위치 원소 삭제하기
•
list.index(data) : 특정 값(data) 가 존재하는 위치를 돌려준다.

2. 정렬과 탐색(Sorting & Searching)

선택 정렬

•
탐색 범위에서 최소값을 찾은 후, 그 값을 범위의 가장 앞으로 보내면서 정렬하는 정렬법입니다.
동작 순서
예시 코드
시간 복잡도

버블 정렬

•
현재 요소와 다음 요소를 비교하며, 큰 값을 뒤로 옮겨준다.
•
이 과정을 반복하여 가장 큰 요소를 범위의 가장 뒷 부분에 보내며 정렬하는 정렬법입니다.
동작 순서
예시 코드
시간 복잡도

삽입 정렬

•
각 모든 요소를 이미 정렬된 앞 부분과 비교하여, 현재 요소의 적합한 위치를 찾아 삽입하여 정렬하는 정렬법입니다.
동작 순서
예시 GIF
예시 코드
시간 복잡도

퀵 정렬

•
정렬 범위 중 하나의 피벗을 선택 후, 피벗 보다 작은 배열과 큰 배열로 나누고 이 배열들을 다시 재귀적으로 정렬하는 정렬법입니다.
동작 순서
예시 코드
시간 복잡도
퀵 정렬을 효과적으로 사용하기 위한 피벗 설정

병합(합병) 정렬

•
전체 원소를 하나 단위로 분할 후, 원소를 각각 비교하며 병합하는 과정에서 정렬하는 정렬법입니다.
동작 순서
예시 GIF
예시 코드
시간 복잡도

퀵 선택

동작 순서
예시 코드

정렬 관련 함수 & 메서드

•
sorted(list,reverse=boolean) : 정렬된 리스트를 반환 (기존 list 는 변화 없음)
•
list.sort(reverse=boolean) : 리스트를 정렬함
key값에 lambda 식을 설정하여 원하는 정렬 조건을 지정
람다 사용법 : lambda 인자 : 표현식

요소의 길이를 기준으로 정렬

list1 = ['test1', 'esttest', '12test'] # 요소의 길이를 기준으로 설정 list1.sort(key=lambda x: len(x)) # ['test1', '12test', 'esttest'] print(list1)
Python
복사

특정 레코드를 기준으로 정렬

list1 = [ {'name':'Jamie', 'age':35}, {'name':'Alfredo', 'age':15}, {'name':'Jessi', 'age':26}, ] # 'name' 레코드를 기준으로 정렬 list1.sort(key=lambda x: x['name']) # [ # {'name': 'Alfredo', 'age': 15}, # {'name': 'Jamie', 'age': 35}, # {'name': 'Jessi', 'age': 26} # ] print(list1)
Python
복사

탐색 관련 개념

선형 탐색 & 순차적 탐색 [ O(n)O(n) ]

리스트의 요소들을 처음부터 순차적으로 탐색하여 원하는 값을 찾는 방법이다.
원하는 값이 발견되지 않을 경우 배열에 있는 모든 원소를 전부 검사한다.

이진 탐색 [ O(logN)O(logN) ]

크기순으로 정렬된 성질을 이용하기 때문에 이미 정렬되어 있는 배열에서 사용할 수 있는 방법이다.
배열의 중간의 양옆 값을 확인하여, 원하는 데이터가 어디에 속하는지 점점 좁혀나가는 방법이다.
# 원하는 값이 90 # 원하는 값이 50(1차 탐색 중간 값)보다 큰 상황, 2차 탐색 시 51(lower) ~ 100(upper) 탐색 1 2 3 4 5 ... 47 48 49 50 51 52 53 ... 99 100 # 원하는 값이 75(2차 탐색 중간 값)보다 큰 상황, 2차 탐색 시 75(lower) ~ 100(upper) 탐색 51 52 53 ... 74 75 76 ... 99 100 # 원하는 값이 87 (3차 탐색 중간 값)보다 큰 상황, 2차 탐색 시 87(lower) ~ 100(upper) 탐색 75 76 ... 86 87 88 ... 99 100 ... 반복
Plain Text
복사
배열의 크기가 커질수록 동작시간이 기하급수적으로 커지는 선형 탐색 & 순차적 탐색에 비해 이진 탐색 방식은 배열의 크기가 동작시간에 큰 영향을 주지 않는다.
하지만, 이미 정렬된 배열이 우선적으로 필요하기 때문에 일회성으로 사용되는 데이터에서 값을 찾을 때 보다 주기적으로 데이터 탐색이 필요한 데이터 목록에서 사용하면 좋다.
왜냐하면 일회성으로 탐색 후 사용하지 않는 데이터에서 굳이 정렬을 추가로 해줄 필요는 없기 때문이다.
예시 코드 (반복문을 이용한 탐색)
예시 코드 (재귀를 이용한 탐색)

3. 재귀 알고리즘(Recursive Algorithms)

재귀 알고리즘이란

•
같은 알고리즘을 반복하여 사용하며 문제를 푸는 방법이다.
•
특정 알고리즘 이름이 아니다. 하나의 방법을 말하는 것이다

재귀 호출의 종결 조건

재귀 알고리즘을 사용하기 위해서는 해당 호출의 종결조건(Trivial case)이 중요하다.
만약 종결조건을 지정하지 않는다면 무한하게 알고리즘을 호출하기 때문이다.
def sum(n): # 종결조건 if n <= 1: return 1 # 종결조건에 부합하지 않는 경우 재귀 호출 else: return n + sum(n-1) # 4 + 3 + 2 + 1 # 10 출력 print(sum(4))
Python
복사
재귀 호출의 형태(Recursive version)에는 그에 대칭되는 반복적인 형태(Iterative version)이 존재합니다.
둘은 복잡도는 동일하지만, 문제에 따라 서로 효율적인 경우가 다릅니다.
하지만, 반복적으로 동일한 함수를 많이 호출하기 때문에 효율성 측면에서는 재귀 호출이 불리한 경우가 많다.

하노이의 탑

재귀 알고리즘의 대표적인 문제로, 옛날 다른나라분들이 즐기시던 놀이(?) 라고 한다.
해당 예시를 잘 숙지하면 재귀에 대한 적용법에 큰 도움이 될 것이다.
하노이의 탑을 잘 설명해주시고 알고리즘으로 적용하는 방법도 상세히 적어주신 블로그 링크를 남긴다.
예시
하노이탑 알고리즘
30층짜리 하노이탑을 옮기려면 무려 34년간을 쉬지도 않고 옮겨야 한다. | 하노이탑을 옮기려면 원반을 모두 (2의 n승)-1번만큼 옮겨야 한다. 원반이 3개라면 총 7번을 옮겨야 한다. 마찬가지로 n이 커지면 -1은 큰 의미가 없으므로 하노이탑 알고리즘의 계산 복잡도는 O(2n)으로 표현할 수 있다. 이는 2를 n번 제곱한 값이므로 n이 커짐에 따라 값이 기하급수적으로 증가한다.
https://brunch.co.kr/@younggiseo/139

4. 알고리즘의 복잡도(Complexity of Algorithms)

공간 복잡도(Space Complexity) : 문제를 해결하는데 사용되는 메모리 공간에 대한 복잡도
시간 복잡도(Time Complexity) : 문제를 해결하는데 걸리는 시간에 대한 복잡도
•
평균 시간 복잡도(Average Time Complexity) : 문제를 해결하는데 소요되는 시간의 평균
•
최악 시간 복잡도(Worst-case Time Complexity) : 문제를 해결하는데 가장 긴 시간

시간 복잡도 표기법

Big-O Notation : 어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 방법
Big-O 복잡도 차트 사진
종류
•
O(n)O(n) : 선형 시간 알고리즘
◦
n의 갯수에 비례한다.
•
O(logn)O(log_n) : 로그 시간 알고리즘
◦
문제 해결에 필요한 과정들이 연산마다 줄어드는 알고리즘
•
O(n2)O(n^2) : 이차 시간 알고리즘
◦
문제를 해결에 필요한 단계가 입력 값 n의 제곱과 같다.
◦
예시 : 삽입 정렬
•
O(2n)O(2^n)
◦
문제의 해결에 필요한 단계의 수가 2의 n 제곱 수와 같다.
•
O(nlogn)O(nlog_n) : 병합 정렬 알고리즘
1.
정렬된 데이터를 반씩 나누어 각각 정렬시킨다. ( O(logn)O(log_n) )
2.
정렬된 각 데이터를 두개씩 한데 합친 후, 정렬한다. ( O(n)O(n) )
합치는 과정에서 어떤 식으로 진행되는지 헷갈릴 수 있다. 안경잡이개발자 님의 정리된 블로그 글을 보면 한눈에 이해할 수 있다. https://blog.naver.com/ndb796/221227934987

시간 복잡도 표시 예시

순차적 탐색
•
Average-case: O(n)O(n)
•
Worst-case: O(n)O(n)
•
순차적 탐색은 무조건 처음 ~ 끝까지 확인하기 때문에 동일하다.
삽입 정렬
•
Best case: O(n)O(n)
◦
모두 정렬이 되어 있을 때 확인만 한다.
•
Worst case : O(n2)O(n^2)
◦
모두 역순으로 정렬되어 있을 때, 매번 정렬해줘야한다.

5. 연결 리스트(Linked Lists)

각 원소들을 링크(link)로 연결하여 관리하는 방법이다.
해당 방법을 이용하여 링크를 끊어 원소를 삭제하거나 그 위치에 다른 원소를 삽입할 수 있다.
이 동작은 선형 배열보다 빠른 시간안에 원소의 삽입 / 삭제 동작을 할 수 있어 많이 사용된다.
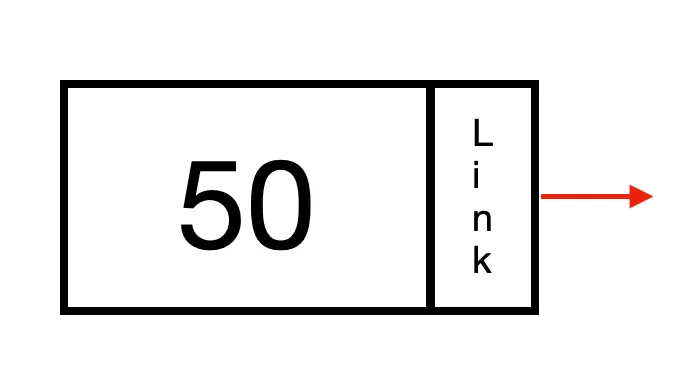
각 원소는 하나의 Node 단위로 관리되며, Data 와 다음 노드를 가르키는 Link(next)로 이루어져있다.
이 노드들이 모이면 연결리스트가 되며 연결리스트의 첫 Node를 Head, 맨 끝의 Node를 Tail 이라 한다.
Head, Tail, 연결리스트의 총 Node 갯수를 알아두면 연결리스트의 추상적 자료구조를 만들 수 있으며 관리에 용이하다.
이는 연속한 위치에 존재하는 일반적인 배열과 가장 큰 차이점으로, 각 연결된 Node가 임의의 위치에 존재가 가능하다는 의미로 해석할 수 있다.
위와 같은 형태의 연결리스트 뿐 아니라, 이전노드 & 다음노드를 확인할 수 있는 양방향 연결 리스트도 존재한다.
양쪽의 Head, Tail 부분은 dummy Node로 채워서 사용하면 Data가 들어있는 Node는 모두 같은 형태(prev, next가 모두 존재하는 형태)이기 때문에 관리가 훨씬 쉽다.

단방향 리스트의 특정 원소 참조 연산

예시로 연결리스트와 각 Node의 클래스는 아래와 같이 정의한다. (빈 연결리스트 일 때)
class Node: def __init__(self, item): self.data = item self.next = None class LinkedList: def __init__(self): # 연결 리스트의 Node 갯수 self.nodeCount = 0 # 만약 Node가 존재한다면 Node 클래스 값이 들어간다. # 즉, curr = self.head 와 같은 코드를 사용한 후 # curr.data / curr.next 등으로 Node를 사용할 수 있다. self.head = None self.tail = None
Python
복사
getNode 함수를 만들어 연결리스트의 원하는 Node를 반환하도록 만들어 봤으며, 아래는 함수의 내용이다.
아래 getNode 함수는 별도로 연결리스트를 인자로 받지만, 연결리스트 클래스(LinkedList)의 내부 함수로 정의하여 사용해도 된다.
# LinkedList : 연결 리스트 # index : 원하는 Node 번호 def getNode(LinkedList, want_index): # 아래 조건 중 하나라도 만족하면 Node Return # 만약 원하는 인덱스 번호가 0이하 # 연결 리스트의 전체 Node 수 보다 클 때 if want_index < 1 or want_index > LinkedList.nodeCount: return None # 시작 노드 인덱스를 1로 시작 curr_index = 1 # 첫 노드 부터 시작 curr = LinkedList.head # 원하는 인덱스 값에 도달할 때 까지 Node 이동 작업 while curr_index < want_index: # 다음 노드로 넘어감 (원하는 인덱스가 아니기 때문에 데이터 조회 X) curr = curr.next # 현재 인덱스 값 +1 curr_index += 1 return curr
Python
복사
함수의 동작 순서는 크게 아래와 같다.
1.
연결리스트의 head를 받아옴(연결리스트가 클래스일 경우 self.head)
2.
원하는 인덱스 번호의 Node 까지 이동 (curr = curr.next)
3.
원하는 인덱스 번호의 Node를 반환 (return curr)
함수 사용 예시
위 함수 내용을 적절히 변경하여, 각 Node의 내용을 출력하게 만들거나 while 문을 사용하여 연결리스트의 길이를 알아내는 등 여려방향으로 응용이 가능하다.

6. 스택(Stacks)

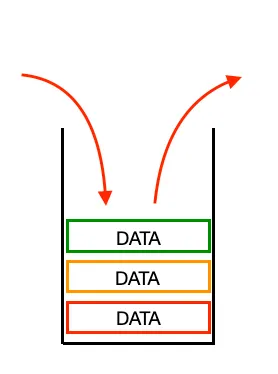
스택은 데이터를 넣은 순서의 역순으로 꺼내서 사용하는 대표적인 LIFO(Last In, First Out) 형태의 자료 구조이다.
일반적으로 삽입 / 삭제 작업은 모두 첫 번째 요소에서 진행되기 때문에 O(1)O(1) 시간 복잡도를 가진다.

스택에서 만들 수 있는 메소드

•
size() : 현재 스택에 들어있는 원소의 갯수를 구한다.
•
isEmpty() : 현재 스택이 빈 스택인지 확인한다.
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
def isEmpty(self): return self.size() == 0
Python
복사
•
push(data) : 데이터 원소 data를 스택에 추가한다.
•
pop(index) : index 번째 원소를 제거 후, 반환한다.
◦
만약 index값이 없다면 맨 마지막 값을 제거 후 반환한다.
•
peek() : 스택에 가장 나중에 저장된 원소를 반환한다. 하지만 pop() 과 다르게 실제로 제거하지는 않는다.

스택 관련 에러

•
스택 언더플로우(stack underflow) : 비어있는 스택에서 데이터 원소를 꺼낼 때
•
스택오버플로우(stack overflow) : 꽉 찬 스택에 데이터 원소를 추가하려할 때

7. 큐(Queues)

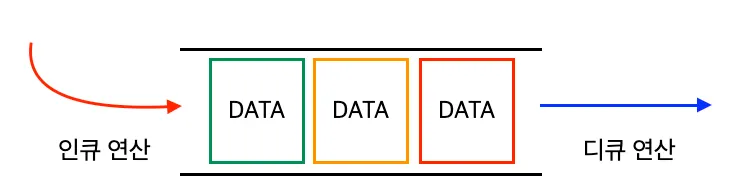
큐는 데이터를 넣은 순서대로 꺼내서 사용하는 대표적인 FIFO(First In, First Out) 형태의 자료 구조이다.
큐는 데이터를 넣을 때 한 쪽 끝에서 넣어야 하며 꺼낼 때에는 넣은 곳에서 반대 쪽에서 꺼내야한다.
이때 데이터를 넣는 작업을 인큐 연산(enqueue), 데이터를 꺼내는 연산을 디큐 연산(dequeue)이라고 한다.
일반적으로 삽입 작업은 큐의 끝에서, 삭제 작업은 첫 번째 요소에서 진행되기 때문에 O(1)O(1) 시간 복잡도를 가진다.

큐에서 만들 수 있는 메소드

•
size() : 현재 큐에 들어있는 원소의 갯수를 구한다.
•
isEmpty() : 현재 큐가 빈 큐인지 확인한다.
•
enqueue(data) : 데이터 원소 data를 큐에 추가한다.
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
def enqueue(self, data): return self.data.append(data)
Python
복사
•
dequeue() : 원소를 제거 후, 반환한다.
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
def dequeue(self): return self.data.pop(0)
Python
복사
•
peek() : 큐에 가장 나중에 저장된 원소를 반환한다. 하지만 dequeue() 과 다르게 실제로 제거하지는 않는다.
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
def peek(self): return self.data[0]
Python
복사

덱(deque)

double-ended queue 의 줄임말인 deque는 collections 모듈에서 제공하는 데이터 구조다.
양쪽 끝에서 요소를 추가/제거 가능한 큐이며, 스택과 큐의 기능을 모두 갖추고 있는 유연한 데이터 구조이다.
•
양방향 연결 리스트를 사용하여 구현되었기 때문에, 해당 데이터 구조의 특징을 갖는다.
•
양방향 모두 데이터 추가 및 제거 시, O(1)O(1) 의 시간 복잡도가 발생한다.
◦
오른쪽 끝은 스택처럼, 왼쪽끝은 큐처럼 사용할 수 있는 것이다.
•
하지만, 중간 요소의 접근 및 추가/삭제는 O(1)O(1) 이 아닌 O(n)O(n) 이다.
◦
양방향 연결 리스트는 일반적인 선형구조(Array)와 다르게 논리적 위치와 실제 물리적 위치가 다르다.
◦
즉, 실제 메모리상 연속적으로 존재하지 않기 때문에 조작이 필요한 요소에 접근하기 위해서는 해당 위치까지 순차적으로 노드에 따라가며 접근해야 한다.
Example

8. 환형 큐(Circular Queues)

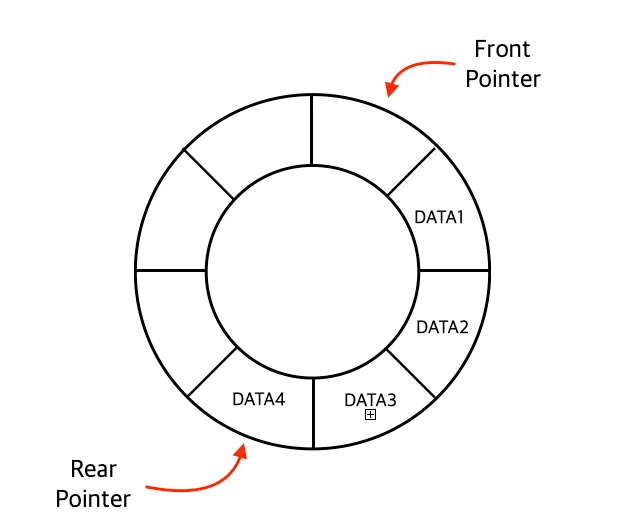
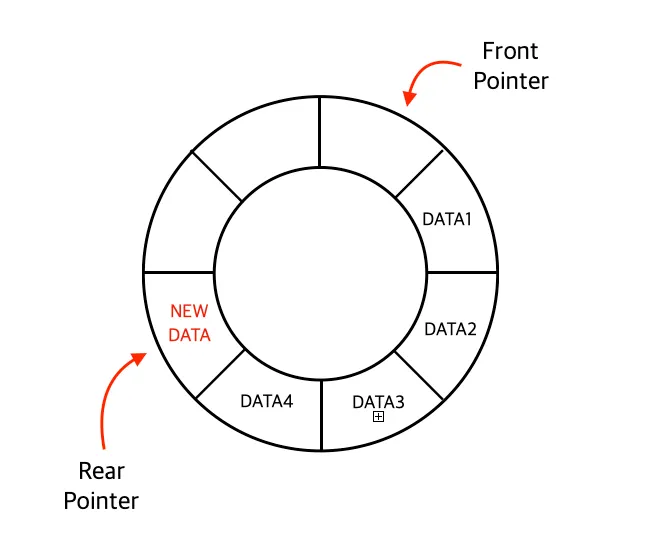
큐의 저장 공간(self.maxCount)을 정한 후, 해당 공간을 돌려가며 사용하는 방식이다.
환형 큐의 저장 공간을 컨트롤하기 위해 Rear(Rear Pointer) 과 Front(Front Pointer) 를 지정하여 사용한다.

환형 큐 에서 데이터 추가 & 삭제

데이터 추가

환형 큐에서 데이터를 추가할 경우 Rear 을 한칸 움직인 후, 해당 포인트 자리에 데이터를 집어넣는다.
이때 Rear Pointer는 아래와 같은 식을 거쳐 변경된다.
# rear pointer 값이 0 ~ (maxCount-1) 값 범위내에서 이동하기 떄문 rear = (rear + 1) % self.maxCount
Python
복사

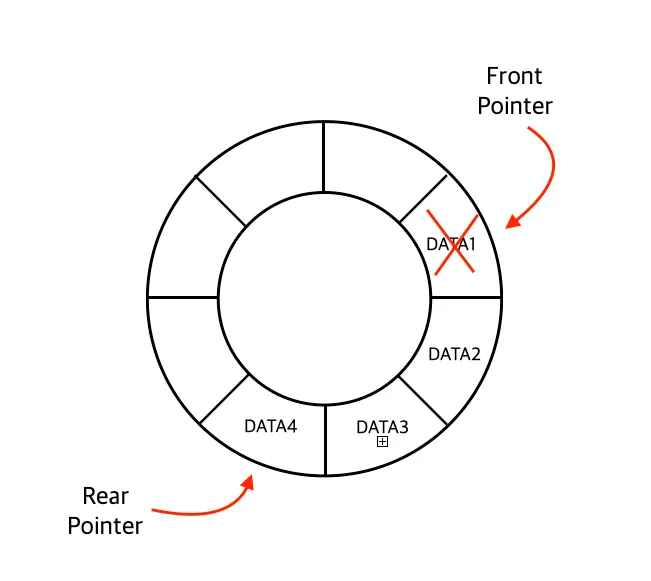
데이터 삭제

환형 큐에서 데이터를 제거할 경우 Front를 한칸 움직인 후, 해당 포인트 자리의 데이터를 제거한다.
이때 Front Pointer는 아래와 같은 식을 거쳐 변경된다.
# front pointer 값이 0 ~ (maxCount-1) 값 범위내에서 이동하기 떄문 front = (front + 1) % self.maxCount
Python
복사

환형 큐 에서 만들 수 있는 메소드

환형 큐에서는 저장공간(self.maxCount)이 정해져 있기 때문에, 큐의 공간이 모두 채워져 있는지 확인하는 함수를 생성한다.
•
isFull() : 현재 큐의 저장공간이 모두 채워져 있는지 확인한다.
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
def isFull(self): return self.count == self.maxCount
Python
복사

9. 우선순위 큐(Priority Queues)

큐의 대표적인 특징인 FIFO(First In, First Out) 를 따르지 않고, 각 원소들의 우선순위를 정하여 해당 우선 순위에 맞춰 데이터를 꺼내는 방식을 사용하는 큐

10. 트리(Trees)

root 노드에서 간선(edge)들이 뿌리처럼 뻗어나가는 구조를 가진 형태이다.

트리 관련 용어

•
Node의 수준(Level)
root 노드에서 간선을 하나씩 거칠 수록 레벨이 하나씩 증가한다.
root 노드가 0 일 경우 간선을 거칠 수록 Level 1, Level 2 ... 로 증가
•
Node의 높이(Height) or Node의 깊이(depth)
Node의 높이 = Node의 최대 수준(Level) + 1
•
부분 트리(서브 트리)
트리에서 특정 노드를 기준으로 가장 아래쪽 자식 노드까지를 묶어 부분 트리라고 한다.
•
Node의 차수(Degree)
자식 Node 수를 나타내며, 이때 자식 트리가 없는 Node들을 leaf Node라고 한다.
•
트리의 시간 복잡도
연산
최선
평균
최악
설명
삽입
O(1)O(1)
O(1)O(1)
O(1)O(1)
특정 노드 아래에 새로운 노드 추가
삭제
O(N)O(N)
O(N)O(N)
O(N)O(N)
삭제가 필요한 노드를 탐색 후 삭제
탐색
O(N)O(N)
O(N)O(N)
O(N)O(N)
탐색이 필요한 노드를 찾는다

11. 이진 트리(Binary Tree)

모든 노드의 차수(자식 노드 수)가 2개 이하인 구조로 이루어진 트리이다.
이러한 구조를 가진 트리는 아래와 같이 재귀적으로 정의할 수 있다.
1.
구조가 루트 노드 + 왼쪽 서브트리 + 오른쪽 서브트리 구조이다.
•
이때 빈 트리도 이진 트리로 간주한다!
2.
왼쪽과 오른쪽 서브트리도 마찬가지로 이진 트리이다.

특별한 구조를 가진 이진트리

1.
포화 이진 트리
•
모든 차수(Level)의 노드들이 모두 2개씩 채워져 있는 이진 트리
•
높이가 kk 일때 노드의 개수가 2k−12^k -1 인 이진트리다.
•
포화 이진트리의 시간 복잡도
연산
최선
평균
최악
설명
삽입
O(1)O(1)
O(logN)O(logN)
O(logN)O(logN)
새로운 노드를 마지막 레벨의 왼쪽부터 삽입 가장 오른쪽 노드에 바로 추가되는 경우, 바로 포화 이진트리의 조건에 맞기 때문에 O(1)
삭제
O(logN)O(logN)
O(logN)O(logN)
O(logN)O(logN)
삭제가 필요한 노드를 탐색 후 삭제
탐색
O(1)O(1)
O(logN)O(logN)
O(logN)O(logN)
탐색이 필요한 노드를 찾는다 탐색 노드가 루트 노드일 경우에는 O(1)
•
포화 이진 탐색 트리를 구성하는 노드의 갯수가 N일때, 트리 높이는 다음과 같다.
◦
N=2(h+1)−1N = 2^{(h+1)}-1 → N은 노드 갯수, h는 높이
▪
2(h+1)=N+12^{(h+1)} = N+1
▪
h+1=log2(N+1)h+1 = log_2(N+1)
▪
h=log2(N+1)−1h = log_2(N+1)-1
▪
즉, 트리의 높이(h)에 비례하여 검색 / 삽입 / 삭제의 시간 복잡도가 증가하는 이진 탐색 트리는 O(logN)O(logN)의 시간 복잡도로 표현할 수 있다.
2.
완전 이진 트리
•
높이가 kk 일 때, 레벨 k−2k-2 까지는 모든 노드가 2개의 자식을 가진 포화 이진트리 상태
•
높이가 kk 일 때, 레벨 k−1k-1(마지막 노드 레벨)를 제외한 모든 노드들은 포화 이진트리 상태이며, 레벨 k−1k-1(마지막 노드 레벨) Node들은 왼쪽부터 순차적으로 채워진다.
•
완전 이진트리의 시간 복잡도
연산
최선
평균
최악
설명
삽입
O(1)O(1)
O(logN)O(logN)
O(logN)O(logN)
새로운 노드를 마지막 레벨의 왼쪽부터 삽입 가장 오른쪽 노드에 바로 추가되는 경우, 바로 완전 이진트리의 조건에 맞기 때문에 O(1)
삭제
O(logN)O(logN)
O(logN)O(logN)
O(logN)O(logN)
삭제가 필요한 노드를 탐색 후 삭제
탐색
O(1)O(1)
O(logN)O(logN)
O(logN)O(logN)
탐색이 필요한 노드를 찾는다 탐색 노드가 루트 노드일 경우에는 O(1)
•
완전 이진 탐색 트리를 구성하는 노드의 갯수가 N일때, 트리 높이는 다음과 같다.
포화 이진트리의 내용과 동일한 내용
◦
N=2(h+1)−1N = 2^{(h+1)}-1 → N은 노드 갯수, h는 높이
▪
2(h+1)=N+12^{(h+1)} = N+1
▪
h+1=log2(N+1)h+1 = log_2(N+1)
▪
h=log2(N+1)−1h = log_2(N+1)-1
▪
즉, 트리의 높이(h)에 비례하여 검색 / 삽입 / 삭제의 시간 복잡도가 증가하는 이진 탐색 트리는 O(logN)O(logN)의 시간 복잡도로 표현할 수 있다.

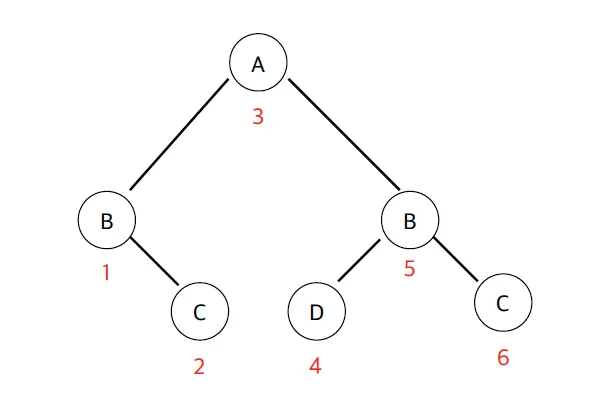
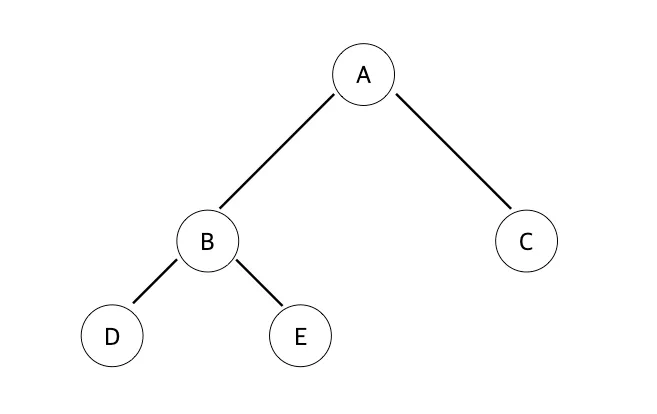
완전 이진트리 예시

루트 노트는 Level 0, 높이가 3 인 노드
가장 마지막 노드 레벨인 D 노드, E 노드가 왼쪽 부터 순차적으로 채워진 상태이다.
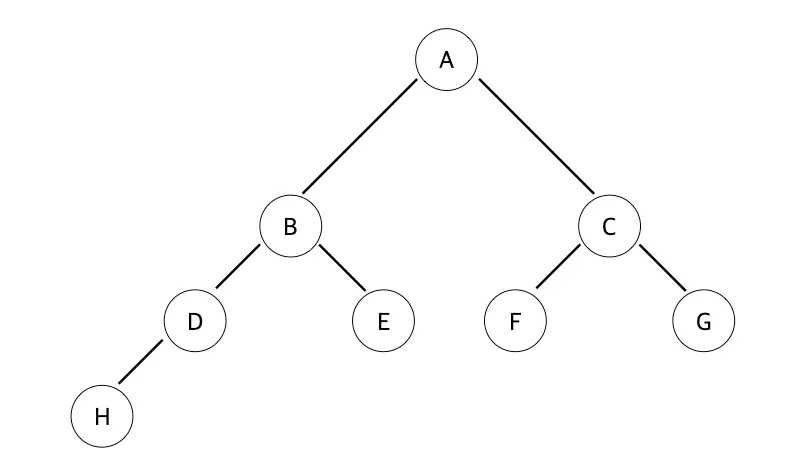
루트 노트는 Level 0, 높이가 4 인 노드
가장 마지막 노드 레벨인 H 노드가 왼쪽 부터 순차적으로 채워진 상태이다.

이진 트리의 자료구조 구현

이진 트리는 아래와 같이 3가지의 요소를 가진 구조이다.
이를 이용하여 아래와 같이 클래스를 정의할 수 있다.
하나의 Node에 대한 정보
class Node: def __init__(self, item): self.data = item self.left = None self.right = None
Python
복사
data : 해당 노드의 값이 들어있는 부분
left : 자식 노드 중 왼쪽에 있는 노드
right : 자식 노드 중 오른쪽에 있는 노드

이진 트리에서 만들 수 있는 메소드

•
size() : 왼쪽 Node의 서브트리 size() + 오른쪽 Node의 서브트리 size()
이때 자식 노드가 None 일 경우 0 반환 (종단 조건)
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
class Node: def size(self): # root 노드 일 때 if self.root: return self.root.size(): else: left_size = self.left.size() if self.left else 0 right_size = self.right.size() if self.right else 0 # 자기 자신의 노드 갯수도 포함 return left_size + right_size + 1
Python
복사
•
소스코드는 해당 강의의 연습문제이기 때문에 작성 X

12. 이진 트리의 순회법(Traversal)

이진 트리에서 순회하는 법은 깊이 우선 순회(depth first traversal)와 넓이 우선 순회(breadth first traversal)로 나뉜다.

깊이 우선 순회(depth first traversal)

그래프의 깊은 부분을 먼저 탐색하는 방법이다. 주로 스택과 재귀함수를 사용하며, 동작 순서는 크게 아래와 같다.
1.
탐색 시작 노드를 스택에 넣기
2.
스택의 최상단 노드에서 인접한 노드 중 방문하지 않은 노드가 있다면 그 노드를 스택에 삽입하고 방문 처리하며, 인접한 노드들 중 방문하지 않은 노드가 없다면 스택에서 최상단 노드를 꺼낸다.
3.
2번 과정을 반복하여 큐가 빈공간이 될때까지 진행합니다.

예시 (낮은 노드를 우선 방문할 때)

깊이 우선 순회에서도 어떤 노드를 먼저 순회하는지에 따라 아래 3가지로 나뉜다.

중위 순회(in-order traversal)

중위 순회는 왼쪽 서브트리 → 본인 노드 → 오른쪽 서브트리를 순서로 순회하는 방식이다.
만약 서브트리의 노드가 오른쪽에만 존재한다면, 본인노드 → 오른쪽 서브트리 순서로 순회한다.
중위 순회에서 만들 수 있는 메소드
•
inorder() : 왼쪽 서브 트리 순회 결과 + 본인 노드 추가 + 오른쪽 서브 트리 순회 결과
python의 리스트에서 지원하지는 않으며, 아래와 같이 만들 수 있다.
class Node: def size(self): # root Node일 경우 if self.root: return self.root: return self.root.inorder() # 순회 결과가 저장되는 리스트 traversal = [] # 왼쪽 서브트리 결과 추가 if self.left: traversal += self.left.inorder() # 본인 노드 추가 traversal.append(self.data) # 오른쪽 서브트리 결과 추가 if self.right: traversal += self.right.inorder() return traversal
Python
복사

전위 순회(pre-order traversal)

전위 순회는 본인 노드 → 왼쪽 서브트리 → 오른쪽 서브트리를 순서로 순회하는 방식이다.
소스코드는 해당 강의의 연습문제이기 때문에 작성 X

후위 순회(post-order traversal)

후위 순회는 왼쪽 서브트리 → 오른쪽 서브트리 → 본인 노드를 순서로 순회하는 방식이다.
소스코드는 해당 강의의 연습문제이기 때문에 작성 X

넓이 우선 순회(breadth first traversal)

노드의 수준(Level)이 낮은 노드를 우선으로 방문한다.
만약 같은 수준의 노드일 때는 부모 노드의 방문 순서에 따라 방문하며, 같을 경우 왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문한다.
넓이 우선 순회는 재귀 방식으로 구현하기 어렵고, 큐를 사용하여 방문 순서를 기록하는 방식을 사용할 수 있다.
순서는 크게 아래와 같다.
1.
탐색 시작 노드를 큐에 넣기
2.
큐에서 해당 노드를 꺼낸 뒤, 인접한 노드 중 방문하지 않은 노드를 전부 큐에 삽입하고 방문 처리
3.
2번 과정을 반복하여 큐가 빈공간이 될때까지 진행합니다.

BFS 예시 코드

13. 이진 탐색 트리(Binary Search Tree)

이진 탐색 트리는 아래의 조건을 만족하는 이진 트리로써, 이진 탐색 알고리즘과 비슷한 성질을 가지고 있다.
•
왼쪽 서브트리에 있는 모든 데이터는 현재 노드의 값보다 작다.
•
오른쪽 서브트리에 있는 모든 데이터는 현재 노드의 값보다 크다.
하지만, 이진 탐색 알고리즘에 비해 공간 소요가 큰 단점이 있지만 데이터 원소의 관리가 편하다는 장점도 있다.
또한 이진 탐색 트리는 선형 탐색과 비슷한 모양, 즉 한쪽 방향으로 쏠린 모양 일 때는 효율적이지 못한다.
•
EX) 1, 2, 3, 4 ,5 순서대로 삽입일 때는 오른쪽으로 쏠린다.
•
EX) 5, 4, 3, 2, 1 순서대로 삽입일 때는 왼쪽으로 쏠린다.

이진 탐색 트리에서 만들 수 있는 메소드

python의 리스트에서 지원하지는 않으며, 직접 만들어 사용해야한다.
•
insert() : 트리에 주어진 데이터 원소를 추가하는 메소드
◦
key 값을 비교하여 왼쪽 / 오른쪽 중 적절한 위치를 정한다.
◦
더 이상 탐색할 필요가 없을 경우 해당 위치에 추가
◦
그 전까진 self.left / self.right 에서 insert() 메소드를 재귀적으로 호출하여 탐색
•
remove() : 특정 원소를 트리에서 삭제하는 메소드
◦
삭제를 원하는 원소가 Leaf Node일 경우 고려
◦
삭제를 원하는 원소의 자식 노드가 하나 존재할 경우 고려
◦
삭제를 원하는 원소의 자식 노드가 두개 존재할 경우 고려
•
lookup() : 특정 원소를 검색하는 메소드
◦
부모 노드(parent)를 인자로 받아 확인하는 작업이 있어야한다.
•
inorder() : 키의 순서로 데이터 원소들을 나열하는 메소드
•
min(), max() : 최소 키, 최대 키를 가지는 원소를 탐색하는 메소드
◦
min() : 왼쪽의 노드만 찾아가면 편하게 구할 수 있다.
◦
max() : 오른쪽의 노드만 찾아가면 편하게 구할 수 있다.

14. B-Tree

기존의 이진트리는 데이터의 삽입, 삭제 등이 편리하지만 한쪽으로 쏠린 모양일때는 효율적이지 못한 탐색 시간을 보여줬다.
이를 개선하기 위해 나온 B-Tree는 데이터의 삽입보단 빠른 조회를 위해 만들어졌다.

B-Tree의 특징

•
차수가 M일 때, 자식 노드의 갯수는 반드시 (M/2)개 이상 & 최대 M개를 가진다.
•
모든 leaf 노드는 같은 레벨이다.
•
노드 내부의 키들은 모두 정렬되어야한다.
•
노드의 추가 시, 매번 그래프의 정렬이 이루어진다.
•
한 노드에 여러 값(키)이 들어갈 수 있다.

예시

•
M = 2
•
1~7 노드를 순서대로 삽입한 B-Tree
노드 삽입 순서 확인
만약 이진 탐색 트리였다면, 한쪽으로 쏠렸을 그래프가 양쪽으로 고루 정렬되어 있다.
이때 이진 탐색트리는 최악의 경우 모든 노드를 탐색하는 O(N)O(N) 시간 복잡도이다.
하지만 B-Tree는 노드 조회 시 최악의 경우에도 시간복잡도는 O(logN)O(logN) 의 복잡도를 가진다.

B-Tree 삽입 / 삭제

•
Node 삽입
1.
새로운 노드는 Root Node에 삽입된다.
2.
Root node수가 넘어서게 된다면, 노드를 분할하고 leaf 노드가 생성됩니다.
이때 노드들의 중간 값이 부모 노드, 나머지 노드들은 중간 값보다 크고 작은지 여부에 따라 좌, 우로 나뉜다.
만약, Node의 최대 노드 가능 수가 짝수일 경우 부모 노드는 왼쪽 그룹 중 가장 큰 수가 된다.
Ex) 1,2,3,4 → 1, 2 / 3, 4 → 2 가 부모 노드가 되며, 1 / 3, 4 로 나뉜다.
3.
이때 2번 과정으로 인해 부모 노드가 1개 늘어나게 되는데, 부모 노드가 최대 수를 넘게 된다면 2번 과정을 해당 레벨에서 반복한다.

15. 힙(Heap)

힙은 완전 이진트리의 한 종류로 주로 정렬이나 여러 데이터들 사이에서 최소 or 최대 값을 탐색할 때 사용되며, 데이터 삽입과 삭제 시간이 빠른게 특징이다.

힙의 성질

1.
힙에는 최대 힙(Max Heap)과 최소 힙(Min Heap)이 존재한다.
2.
최대 힙과 최소힙은 모두 느슨한 정렬 상태이다.
느슨한 정렬이란, 좌 / 우 위치에 따라 데이터의 높고 낮음이 정해지지 않고 각 노드의 레벨에 따라서만 데이터가 정렬된 상태를 말한다.
3.
이전의 이진 탐색 트리와 달리 중복 값을 허용한다.

힙의 종류

최대 힙(Max Heap)

최대 힙은 아래 3가지 조건을 만족하는 힙이다.
1.
상위 노드(부모 노드)가 서브트리의 모든 노드의 값보다 항상 크다.
2.
최대 힙 내의 특정 노드를 루트로 하는 서브트리 또한 최대 힙 상태이다.
3.
완전 이진 트리이다.

최소 힙(Min Heap)

최소 힙은 아래 3가지 조건을 만족하며, 최대 힙(Max Heap)의 반대 버전이라고 생각하면 편하다.
1.
상위 노드(부모 노드)가 서브트리의 모든 노드의 값보다 항상 작다.
2.
최소 힙 내의 특정 노드를 루트로 하는 서브트리 또한 최소 힙 상태이다.
3.
완전 이진 트리이다.

힙 구현하기

 직접 메소드 만들기

•
insert(item) : 새로운 원소를 삽입하는 메소드
1.
트리의 마지막 자리에 임시로 새로운 원소를 저장
2.
부모 노드와 키 값을 비교하여 이동 후 조건 만족 시, 상위로 이동
•
기존 키 값 // 2 을 반복하여 부모 노드 단계로 이동한다.
•
remove() : root node 를 반환 후 힙에서 삭제처리
1.
힙에서 원소 제거 시, 루트 노드에서 하나가 제거된다.
2.
트리 마지막 노드를 임시로 루트 노드 자리에 배치
3.
더 큰 자식 노드와 비교 후, 조건 만족 시 하위로 이동(삽입 단계와 반대)
예시 코드

 모듈을 사용한 힙 구현

•
import heapq : 모듈 임포트
•
heapq.heapify(list) : 리스트를 최소힙으로 만들기
•
heapq.heappush(heap, value) : 힙에 값을 추가하기
•
heapq.heappop(heap) : 힙의 루트 값 꺼내기(최소힙 기준 가장 작은 값)
최대 힙 만들기

최대 / 최소 힙의 응용

우선 순위 큐(priority queue)에서 사용

•
Enqueue 시, 느슨한 정렬을 이루고 있도록 한다.
•
Dequeue 시, 최댓 값을 순서대로 추출 가능

힙 정렬(heap sort)

•
정렬되지 않은 원소들을 아무 순서로 힙에 삽입 가능
•
삽입 후, 빈 힙이 될 때 까지 하나씩 삭제
•
원소들이 삭제된 순서 = 원소들의 정렬 순서

힙의 시간복잡도

•
힙의 데이터 추가 / 삭제 시마다 재정렬의 과정이 필요하다.
◦
이때 비교 횟수는 트리의 높이 만큼이기 때문에, O(logN)O(logN) 이다.
•
힙의 데이터 탐색도 동일하게 트리의 높이 만큼 진행되기 때문에, O(logN)O(logN) 이다.

16. 트라이(Trie) 알고리즘

주로 빠른 문자열의 조회를 위해 사용되며, 비트와 같이 순서가 존재하는 데이터에서도 사용이 가능하다.
각 자식노드에 대한 정보를 모두 저장하기 때문에, 저장공간은 많이 차지하지만 그만큼 빠른 탐색이 가능하다.
시간복잡도는 아래와 같다. N은 문자열 갯수, L은 각 문자열의 길이이다.
•
삽입 : O(N∗L)O(N * L) → 추가하려는 문자열의 길이만큼 데이터 추가가 필요
•
탐색 : O(L)O(L) → 탐색 시, 가장 긴 문자열의 길이 이상으로 탐색하지 않기 때문
•
삭제 : O(L)O(L) → 삭제를 위해, 특정 문자열을 탐색하기 때문

트라이의 구현

트라이는 각 문자의 정보를 담는 Node의 구성으로 이루어진다.
각 Node는 총 3가지 정보를 저장한다.
•
해당 노드의 문자
•
해당 노드의 문자열이 존재하는지 저장
◦
EX) hello 는 h → e → l → l → o 노드를 순서대로 탐색하며, 이때 마지막 o 노드에 hello 문자열에 대한 존재 여부를 저장한다.
◦
문자열 자체를 저장하기도 하고, Boolean 값으로 문자열 존재 여부만 저장하기도 한다.
•
자식 노드의 정보
◦
보통 Dict 형태로 저장하며, {'<Char>' : 'Node_Class'} 형식으로 저장된다.
Example (Trie 파이썬 구현)

 17.그래프

그래프는 트리와 다르게, 계층형 모델이 아니기 때문에 루트 노드라는 개념이 없다.
참고로 트리는 그래프의 한 종류이다. 그래프가 더 큰 개념인 것이다.

무방향 그래프 vs 방향 그래프

무방향그래프

•
간선이 방향을 가지지 않는다.
•
Node간의 관계가 양방향(방향이 존재하지 않기 때문)이다
•
방향이 정해져있지 않아 연결 관계를 표현하는데 사용된다.
•
A — B 로 표현한다.
•
BFS / DFS 모두 O(V+E)O(V + E) 의 시간 복잡도를 가진다
◦
각 노드 방문 O(V)O(V)
◦
각 간선 탐색 O(E)O(E)
Example(무방향 그래프 BFS)
Example(무방향 그래프 DFS)

방향그래프

•
간선이 방향을 가진다
•
Node간의 관계가 일방적(방향이 존재하기 때문)이다
•
방향이 정해져있어 순환 구조를 가지기 쉽다
•
A → B 로 표현한다.
•
BFS / DFS 모두 O(V+E)O(V + E) 의 시간 복잡도를 가진다
◦
각 노드 방문 O(V)O(V)
◦
각 간선 탐색 O(E)O(E)
◦
다만 방향 그래프는 각 노드의 연결관계가 무조건 양방향이 아니기 때문에, 그래프 연결관계 표현 시 다르게 설정하기만 하면 된다.
Example(방향 그래프 BFS)
Example(방향 그래프 DFS)

최소신장트리(MST, Minimum Spanning Tree)

각 노드마다 연결된 간선에 가중치가 존재하는 Spanning 그래프에서, 최소한의 비용으로 모든 노드를 연결하는 문제에서 사용한다.
이때 사용하는 알고리즘은 프림, 크루스칼 알고리즘을 사용한다.
프림, 크루스칼 두 알고리즘은 탐욕법으로 구현할 수 있다.
이때 프림 알고리즘의 시간 복잡도는 O(n2)O(n^2) 이며, 크루스칼 알고리즘의 시간 복잡도는 O(elog2e)O(elog_2e)이다.
따라서, 그래프 내에 간선이 적을 경우(희소 그래프) 크루스칼 알고리즘을, 그렇지 않다면 프림 알고리즘을 사용하면 좋다.

Spanning 그래프란?

신장트리라고도 하며, 그래프의 모든 간선 중 일부를 사용한 트리이며 항상 그래프 전체의 부분집합이 된다.
특징은 크게 2가지가 있다.
1.
신장트리의 간선은 그래프의 모든 정점을 포함한다.
2.
사이클이 발생하면 안되기 때문에, N개의 정점이 존재하는 신장트리는 (N-1)개의 간선으로 구성되어야한다.
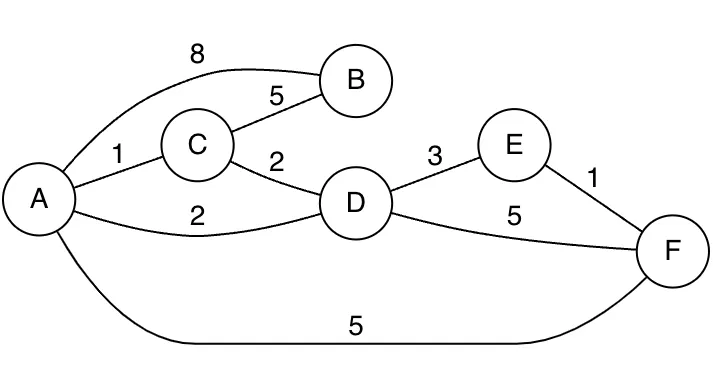
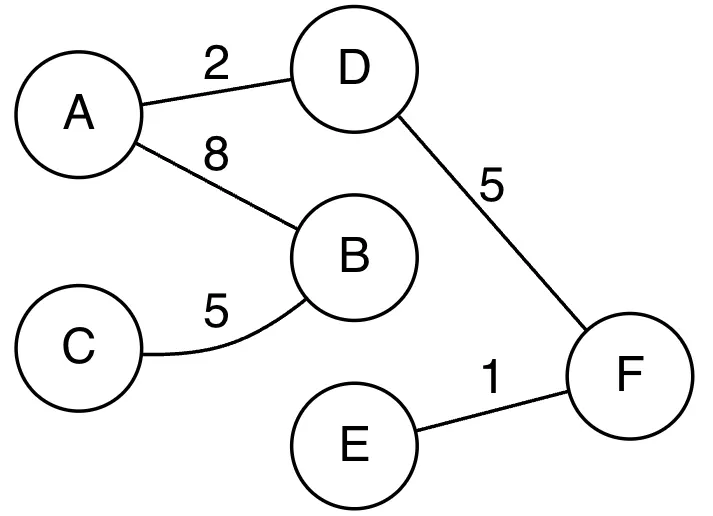
만약 아래와 같은 그래프가 존재할 때, Spanning 그래프(신장트리)는 오른쪽과 같이 표현이 가능하다.
•
전체 그래프
•
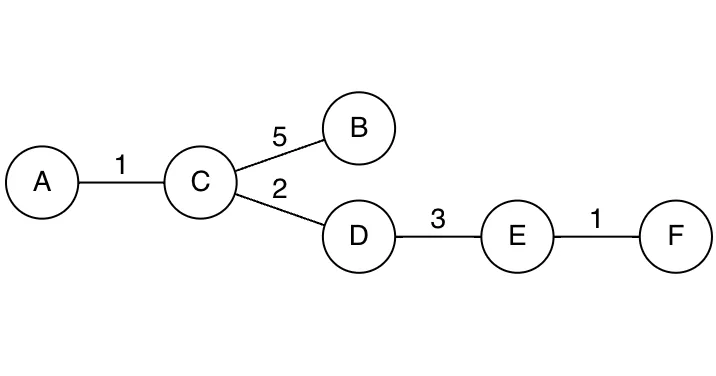
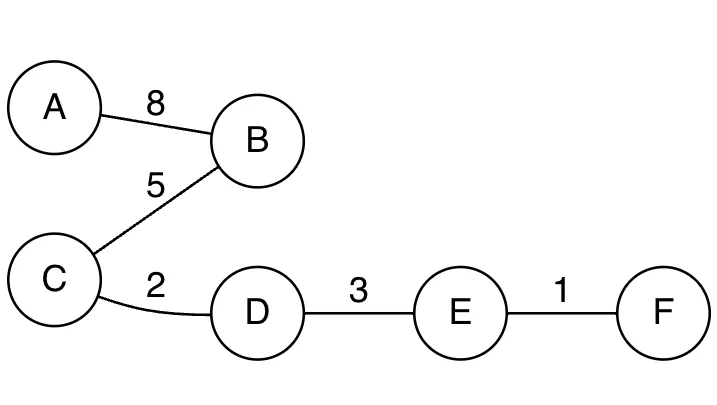
Spanning 그래프(신장트리)
→ 아래와 같이 신장트리의 표현이 가능하다.
내용 참고

프림 알고리즘

시작 노드에서 출발하여, 신장 트리의 집합을 단계적으로 확장한다. 정점을 사용하는 알고리즘이다.
이때, 인접한 노드에서 최저 가중치로 연결된 노드를 신장트리 집합에 추가한다.
또한 해당 노드에 접근하였을 때 필요한 최저 가중치를 별도로 저장한다.
위 과정으로 모든 노드가 하나의 신장트리로 연결되었을 때, 각 노드에 접근하기 위한 최저 가중치를 모두 더하면 MST를 만들기 위한 가장 적은 가중치 합을 구할 수 있다.
•
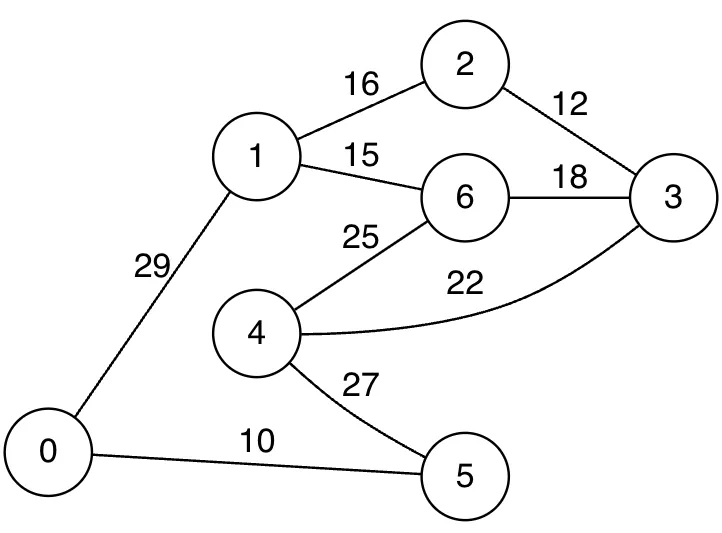
전체 그래프 예시
•
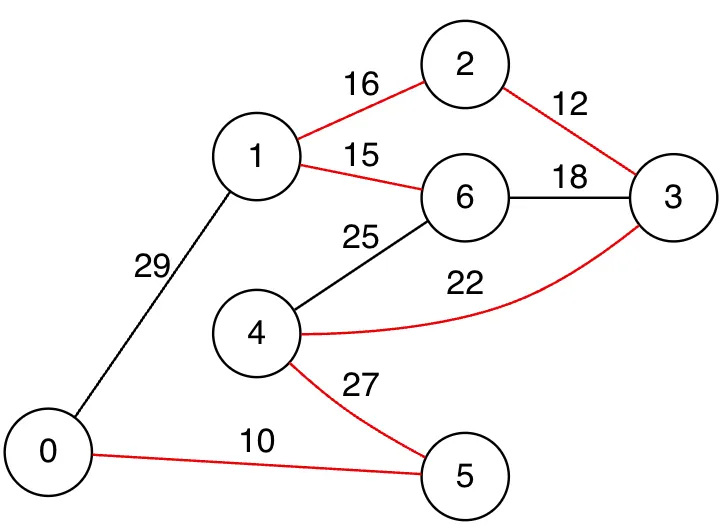
프림 알고리즘을 이용한 MST
소스 코드

크루스칼 알고리즘

그래프의 모든 간선을 오름차순 정렬해놓은 뒤, 싸이클이 존재하지 않도록 정렬된 순서대로 간선을 선택한다.
이도 마찬가지로 정점이 N개일 때, (N-1)개의 간선을 확인했다면 탐색을 종료한다.
작성중…

다익스트라 알고리즘 (Dijkstra) & 벨만-포트 알고리즘 (Bellman-Ford)

다익스트라 알고리즘 (Dijkstra)

각 노드마다 연결된 간선에 가중치가 존재하는 그래프에서, 출발 노드에서 도착 노드까지의 최단 경로를 찾기위한 알고리즘이다.
양방향 예시
단방향 예시
소스코드

벨만-포드 알고리즘 (Bellman-Ford)

다익스트라 알고리즘과 유사하다.
하지만 다익스트라와 다르게 가중치가 음수일 때도 사용 가능하며, 이때 발생가능한 음수 사이클을 탐지한다.
음수 사이클이란? 음수 가중치를 계속 더해주면서, 최단 거리를 정확히 구할 수 없는 상태
다익스트라 알고리즘에서는 V-1 번 반복했다. → V-1번 반복하면 최단 경로는 다 구해진다.
하지만 벨만-포드 알고리즘은 음의 사이클이 일어나는지 확인하기 위해 마지막에 1번 더 반복한다.
마지막 반복에서도 최소 경로가 바뀐다면, 이는 음수 사이클의 존재가 있음을 알 수 있다.
즉 벨만-포드 알고리즘은 다익스트라 알고리즘 + 음수 사이클 확인 알고리즘이라고 할 수 있다.
그래서 예시에서는 음의 사이클인 경우에는 -1 을 반환한다. → 이는 문제의 조건마다 다를 수 있다.
예시 그래프 (음수 사이클 존재X)
예시 그래프 (음수 사이클 존재 O)
소스코드
만약 음수 사이클 탐지가 없다면?
예시 & 코드 참조

플로이드-워셜 알고리즘

그래프의 모든 노드쌍에 대한 최단거리를 모두 구하는 알고리즘이다.
시간복잡도가 O(N3)O(N^3) 이기 때문에, 노드와 간선이 적은 상황에서 사용하는 것이 좋다.
두 노드의 최소 거리는 Dab=min(Dab,Dak+Dkb)D_{ab} = min(D_{ab}, D_{ak} + D_{kb}) 식에 따라 갱신한다. 이때 DabD_{ab} 는 기존의 aa → bb 거리를 나타낸다.
즉, 새로운 DabD_{ab} 는 기존의 aa → bb 거리와 kk라는 중간 노드를 거친 (aa → kk 거리 + kk → bb 거리) 중 짧은 거리를 가진 값을 넣는다.
예시 그래프
예시(노드의 이름이 정수가 아니어서 배열을 이용한 연결 정보 저장이 어려울 때 사용)
예시(최대 노드 값과 정수형의 이름을 가진 일반적인 그래프일 때)

알고리즘 문제 풀이를 위한 입력과 출력 팁

 문제에서 요구하는 알고리즘을 찾는 팁

코딩테스트 팁 (python)
1. 아스키코드 변환 ord(value) # 역으로는 chr 2. 조합 from itertools import combinations from itertools import permutations list(map(''.join,combinations( arr , 1 ))) 3. 절대값 abs(value) 4. 문자열 리스트 합치기 text = ''.join(arr) 5. 최대 공약수 import math math.gcd(21, 14) #7 6. 펙토리얼 factorial import math math.factorial(5) #120 7.
https://velog.io/@tlsehguddn23/%EB%AC%B8%EC%A0%9C-%EC%A0%95%EB%A6%AC

문제의 정답 예시 값 입력 받는법

코딩테스트의 문제에서는 예제 입력 / 예제 출력 으로 나뉘어 정답의 예시를 보여준다.
각 문제마다 띄어쓰기 / 엔터 등 다양한 구분자로 입력 값을 구분하기 때문에, 각 상황에 맞는 테스트 값(예시 값) 입력 법을 알아두면 편하다.
본인은 파이썬을 주로 사용하여 코딩테스트를 준비하기 때문에 python3 를 기준으로 작성하였다.

띄어 쓰기로 입력 값이 구분되는 경우

예제 입력이 오른쪽과 같은 경우이다.
이럴 경우에는 split() , map() 함수를 사용한다.
예제 입력 4 7
Plain Text
복사
input().split() 를 사용하여 띄어쓰기로 구분된 값을 나눈 후, map() 함수를 사용하여 int형으로 변환
num1, num2 = map(int, input().split()) # 입력 값 확인 print("num1 : {}".format(num1)) print("num2 : {}".format(num2))
Python
복사
map(int, input().split()) 은 아래와 같은 과정이다.
# input().split() 값 -> ['4', '7'] value = input().split() # map()을 사용하여 리스트 요소를 int로 변환 data = map(int, value) # 해당 map 객체를 이용하여 여러 변수에 값 동시 저장 num1, num2 ... = data
Python
복사

줄바꿈으로 값을 구분하는 경우

예제 입력이 오른쪽과 같은 경우이다.
이럴 경우에는 한 줄씩 input() 해주면 된다.
예제 입력 472 385
Plain Text
복사
num1 = input() num2 = input() # 입력 값 확인 print("num1 : {}".format(num1)) print("num2 : {}".format(num2))
Python
복사

더 빠르게 입력받는 방법

input() 으로 입력 받을 경우 상당히 느리다고 한다.
그래서 파이썬 기본 내장 모듈인 sys 모듈의 sys.stdin.readline() 함수를 사용하여 입력받으면 더 빠르다.
import sys # 입력 행 갯수 N = int(input()) # 입력 행 만큼 반복 for _ in range(N): # input() 대신 sys.stdin.readline()을 사용 A, B = map(int, sys.stdin.readline().split()) print(A, B)
Python
복사

결과 값 출력 방법

코딩테스트의 문제에서는 예제 입력 / 예제 출력 으로 나뉘어 정답의 예시를 보여준다.
간단한 문제는 아래와 같은 방법으로 여러줄의 print 문을 사용하지 않고 1-2줄에 정답 출력이 가능하다.

특정 변수들을 여러 수식을 사용하여 여러줄로 출력할 경우

이 문제와 같이 입력받은 특정 변수를 여러 수식의 결과를 출력하는 문제일 때, 각 수식의 결과마다 print 을 사용할 수 밖에 없게되며 이는 코드가 길어지는 원인이 된다.
•
예제 문제 내용
두 자연수 A와 B가 주어진다. 이때, A+B, A-B, A*B, A/B(몫), A%B(나머지)를 출력하는 프로그램을 작성하시오.
•
출력 값
첫째 줄에 A+B, 둘째 줄에 A-B, 셋째 줄에 A*B, 넷째 줄에 A/B, 다섯째 줄에 A%B를 출력한다.
일반적으로 print 함수를 사용하여 각 수식의 결과를 출력하면 다음과 같다.
print 함수가 하나의 값을 출력한 후, 기본적으로 개행을 하기 때문에 아래와 같이 작성한다.
A, B = map(int, input().split()) print(A+B) print(A-B) print(A*B) print(A//B) print(A%B)
Python
복사
하지만 print 함수의 sep 옵션을 사용하여 한줄에 출력하고자 하는 여러 값을 모두 적은 후, 구분자를 설정할 수 있다.
A, B = map(int, input().split()) print(A+B, A-B, A*B, A//B, A%B, sep='\n')
Python
복사

출력과 조건문 동시 사용법

기존에는 조건문을 사용할 때, 조건에 따라 print 해주는 값을 일일히 설정해줘야했다.
조건이 길거나 출력이 필요한 결과 값이 그리 긴 상태가 아니라면 한줄에 축약하는거도 깔끔한 코드를 작성하는데 하나의 방법이 될 수 있다.
•
예제 문제 내용
두 정수 A와 B가 주어졌을 때, A와 B를 비교하는 프로그램을 작성하시오.
•
출력
첫째 줄에 다음 세 가지 중 하나를 출력한다. - A가 B보다 큰 경우에는 '>'를 출력한다. - A가 B보다 작은 경우에는 '<'를 출력한다. - A와 B가 같은 경우에는 '=='를 출력한다.
일반적인 방법으로 각 조건문의 결과를 출력하면 다음과 같다. 각 조건마다 print 함수를 일일히 설정해야 한다.
A, B = map(int, input().split()) if A > B: print(">") elif A < B: print("<") elif A == B: print("==")
Python
복사
하지만, 아래와 같이 print 문 안에서도 조건식을 직접 작성이 가능하다.
2-3개 정도의 간단한 조건일 경우 아래와 같이 사용하면 좋을 듯 하다.
A, B = map(int, input().split()) # print([참 출력 값] if [조건] else [거짓 출력 값]) # 거짓 출력 값에 추가적인 조건이 또 들어갈 수 있다. # print([참 출력 값] if [조건] else [참 출력 값] if [2차 조건] else [거짓 출력 값]) print(">" if A > B else("<" if A < B else "=="))
Python
복사

함수 정리

순열과 조합

순열

서로 다른 nn개에서 서로 다른 rr개를 선택하여 일렬로 나열하는 것
nPr=n∗(n−1)∗(n−2)∗...∗(n−r+1)=n!(n−r)!nPr = n * (n-1) * (n-2) * ... * (n-r+1)=\cfrac{n!}{(n-r)!}
from itertools import permutations data = ['1', '2', '3', '4'] result = list(permutations(data, 3)) # [('1', '2', '3'), ('1', '2', '4'), ... ('4', '2', '3'), ('4', '3', '1'), ('4', '3', '2')] print(result)
Python
복사

중복 순열

순열에서 중복을 허용한 경우
n∏r=nrn∏r = n^{r}
from itertools import product data = ['1', '2', '3', '4'] result = list(product(data, repeat=2)) # [('1', '1'), ('1', '2'), ('1', '3'), ('1', '4'), ... ('4', '2'), ('4', '3'), ('4', '4')] print(result)
Python
복사

조합

서로 다른 nn개에서 순서를 고려하지 않고 rr개를 선택한 것
nCr=n∗(n−1)∗(n−2)∗...∗(n−r+1)r!=n!r!(n−r)!nCr = \cfrac{n * (n-1) * (n-2) * ... * (n-r+1)}{r!}=\cfrac{n!}{r!(n-r)!}
from itertools import combinations data = ['1', '2', '3', '4'] result = list(combinations(data, 3)) # [('1', '2', '3'), ('1', '2', '4'), ('1', '3', '4'), ('2', '3', '4')] print(result)
Python
복사

중복 조합

조합에서 중복을 허용한 경우
nHr=n+r−1CrnHr = {\scriptstyle n+r-1}Cr
from itertools import combinations_with_replacement data = ['1', '2', '3', '4'] result = list(combinations_with_replacement(data, 2)) # [('1', '1'), ('1', '2'), ('1', '3'), ... ('2', '4'), ('3', '3'), ('3', '4'), ('4', '4')] print(result)
Python
복사
개인적으로 만들어본 순열 함수

코딩 테스트 문제 정리

주로 백준 사이트나 프로그래머스 사이트에서 코딩 테스트 문제를 많이 공부한다고 한다.
특히 백준 사이트는 문제가 매우 많기 때문에 본인처럼 막 시작한 사람은 어떤 문제를 풀어봐야할지 고민이었는데, 감사하게도 아래 블로그에서 잘 정리해 주셨다.
백준으로 코딩 테스트를 준비하는 사람은 아래 블로그를 참고하면 아주 좋을 것 같다.
코딩테스트 대비를 위한 백준 문제 추천
작년 한 해 수많은 코딩테스트를 직접 경험하고 후기를 들으면서 유사문제, 같은 아이디어로 풀어야 하는 백준 문제를 모아서 코딩테스트 고득점 kit 글을 작성하였습니다. 빠른 취뽀를 위하여 취업준비 기간 양질의 문제를 풀어보는 것이 중요하다고 생각합니다. Kakao, Naver, Line, NHN 등등 직접 출제하는 회사가 아닌 외주문제의 경우 백준과 유사한 문제가 많이 등장합니다.
https://covenant.tistory.com/224

그래프 그리는 사이트

여러 형태의 그래프를 그릴 수 있는 사이트이다.
아래는 노드로 이루어진 그래프를 그리는 사이트이다.
Graphviz Visual Editor
A web application for interactive visual editing of Graphviz graphs described in the DOT language
http://magjac.com/graphviz-visual-editor/
strict graph → 방향 없는 그래프
digraph 또는 graph → 방향있는 그래프